1° Линеарна функција

График функције је права чији је општи (експлицитни) облик:  при чему је- коефицијент правца праве (где јеугао према позитивном смеру х-осе), а n слободан члан (одсечак који права одређује на y-оси тј. одстојање пресека А(0,n) праве и y-осе од координатног почетка).

2° Квадратна функција

График функције, чији је општи облик:, је парабола. Нуле функције су реална решења једначине(ако она постоје), тј., за ≥ 0, где је D дискриминанта. Теме графика функције је тачка.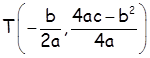
У зависности од знака коефицијента а и дискриминанте D разликујемо шест карактеристичних случајева.

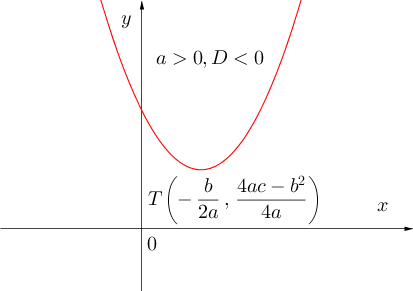
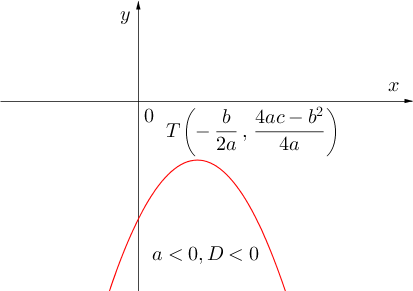
 3° Функције облика

Ако је n паран број, функцијаје дефинисана.
Ако је n непаран број, функцијаје дефинисана за свако х.

4° Функције облика

График функције је хипербола, дефинисан за. Асимптоте функције су у-оса и х-оса.


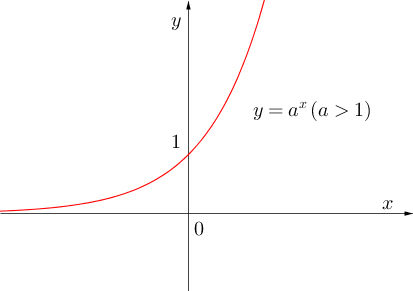
5° Експоненцијална функција

То је функција облика. Функција је дефинисана и позитивна за.

6° Логаритамска функција

То је функција облика. Дефинисана је за. Нула функције је.

7° Тригонометријске функције

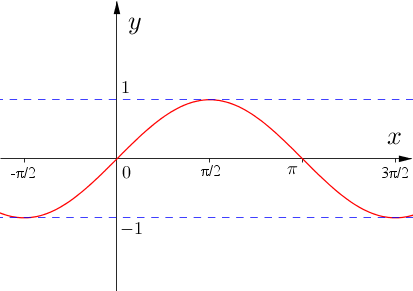
Функција  
- дефинисана је за
- период је
-за
-, за
-, за
- функција је непарна

Функција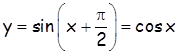  
-дефинисана је за
- период је
- за
- , за
- , за
- функција је парна

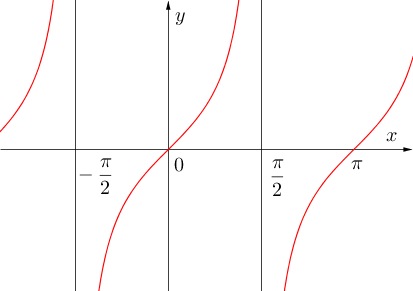
Функција
- заније дефинисана и у тим тачкама има вертикалне асимтоте
- период је
- за
- функција је моното растућа за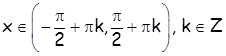

- функција је непарна

Функција
- заније дефинисана и у тим тачкама има вертикалне асимтоте
- период је
- за
- функција је моното опадајућа за

- функција је непарна 

8° Функција

График функције је померен у односу на координатни почетак, и то улево ако је, а у десно ако је. Основни период је. Нуле функције добијамо из једначине. Ако јефункција има максималну вредностза, а минималнуза.

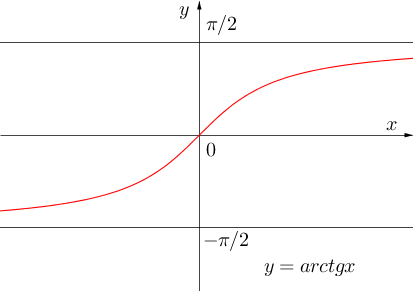
9° Инверзне тригонометријске функције,- функције

- Инверзна функција функције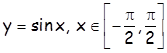је
- Инверзна функција функцијеје
- Инверзна функција функцијеје
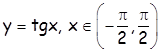- Инверзна функција функцијеје