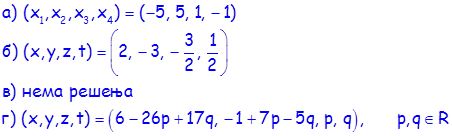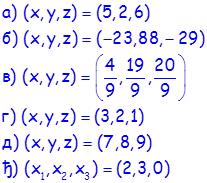Системи линеарних једначина
Систем од m једначина са n непознатих је конјункција једначина

1. Гаусов поступак. Ако је у систему (1)![]() треба да елиминацијом непознате
треба да елиминацијом непознате![]() из друге, треће, ..., m - те једначине добијамо еквивалентан систем
из друге, треће, ..., m - те једначине добијамо еквивалентан систем
где је
Настављајући овај поступак систем сводимо на еквивалентан систем „дијагоналног облика“.
2. Крамерова теорема. Нека је дат систем од n једначина са n непознатих
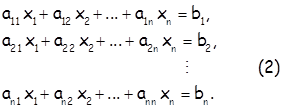
Нека је D детерминанта овог система, а ![]() детерминанте добијене заменом i - те колоне из D елементима
детерминанте добијене заменом i - те колоне из D елементима![]() . Тада:
. Тада:
1° Ако је![]() , систем има јединствено решење:
, систем има јединствено решење:
![]()
2° Ако је![]() и бар једна од детерминанти
и бар једна од детерминанти![]() различита од нуле, систем нема решења.
различита од нуле, систем нема решења.
3° Ако је![]() , Крамерова теорема не даје никакав одговор о решењима система (2). Систем може да има или бесконачно много решења, или да уопште нема решења. У овом случају најбоље је да се систем решава Гаусовим поступком (в. пример у задацима 532 и 533).
, Крамерова теорема не даје никакав одговор о решењима система (2). Систем може да има или бесконачно много решења, или да уопште нема решења. У овом случају најбоље је да се систем решава Гаусовим поступком (в. пример у задацима 532 и 533).