Примедба 1. Приближно одређивање корена дате једначине
(1)![]()
састоји се од два корака:
1° утврђивање што мањег интервала у коме се налази један и само један корен једначине (1);
2° израчунавање приближне вредности корена са датим степеном тачности.
Примедба 2. Метода сечице (метода тетиве). Ако је функција![]() непрекидна у интервалу
непрекидна у интервалу![]() и
и![]() , при чему је
, при чему је![]() за
за![]() , тада једначина (1) има један и само један корен
, тада једначина (1) има један и само један корен![]() у интервалу
у интервалу![]() . Заменом криве
. Заменом криве![]() тетивом која садржи тачке
тетивом која садржи тачке![]() и
и![]() добијамо прву апроксимацију корена
добијамо прву апроксимацију корена
(2)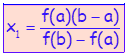
Примењујући даље тај поступак на интервал![]() или
или![]() , у зависности од тога да ли је
, у зависности од тога да ли је![]() или
или![]() , добија се друга приближна вредност
, добија се друга приближна вредност![]() , итд.
, итд.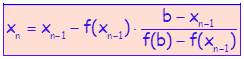
Примедба 3. Низ бројева![]() конвергира ка корену, тј.
конвергира ка корену, тј.![]() .
.
Примедба 4. Њутнова метода (метода тангенте): Ако је![]() и
и![]() у интервалу
у интервалу![]() и
и![]() , онда се поступна апроксимација
, онда се поступна апроксимација![]() корена
корена![]() једначине (1) одређује формулама
једначине (1) одређује формулама
(3) .
.
Примедба 5. Из дате претпоставке низ![]() је монотон и
је монотон и![]() .
.
Примедба 6. Методе итерације: Ако се једначина (1) може трансформисати на облик![]() , и ако се пође од почетне вредности
, и ако се пође од почетне вредности![]() која припада интервалу
која припада интервалу![]() , добија се низ бројева
, добија се низ бројева![]() На овај начин
На овај начин![]() .
.
Ако је![]() , онда је
, онда је![]() .
.

